Все скажут, что единство времени, пространства, энергии и материи это всё впервые было сформулировано в Общей Теории Относительности А.Эйнштейна, но если внимательно рассмотреть по законам математического анализа формулу закона Всемирного притяжения И. Ньютона, то окажется, что это заключено и в его законе:
Fj= G*Mi*Mj/R^2 [1]
Поделив обе части уравнения на Mi, зная, что Fj=Mj*aj
aj = G*Mi/R^2 [2]
По этой формуле рассчитывается ускорение тел не имеющих вращения друг относительно друга. При наличии вращения тел в них появляются приливные ускорения, производные от гравитационных, вызванные разным удалением точек тел от источника гравитации.
w = (aj)`
В классической механике время обозначается (t), пространство характеризуется расстоянием (R), энергия пропорциональна угловой скоростью вращения (ω)[E = mV^2/2 + m(ω*R)^2/2 = mV^2 =mc^2|], материя характеризуется массой (M):
Mi = ρi*V i
ρ-плотность вещества, которая является функцией нескольких переменных и прежде всего радиуса тела (Ri),температуры (Ti), давления (Pi)…;
ρi = f( Ri,, Ti, Pi, …) полная производная от этого выражения будет:
(ρi)` = f( Ri,, Ti, Pi,)`R +(f( Ri,, Ti, Pi,)`T+(f( Ri,, Ti, Pi,)`P…
В условиях макромира плотность вещества обычно принимают постоянной, но в микромире пренебрегать дифференциацией плотности уже нельзя.
V i- объем тела. Для упрощения вопроса рассматриваются шарообразные тела, объем которых Vi = 4/3πRi^3 [фиг. 1] .
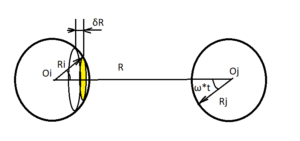
С изменением расстояния между телами происходит изменение взаимодействующих масс, пропорционально изменению объема с изменением расстояния ;
δ Vi -является функцией переменных (ω),(t),(R)
Изменение объема тела (δ Vi) в зависимости от изменения расстояния между телами;
δ Vi = δSi*δR = π (Ri*sin ωi*t+φ)^2*δR производная этого выражения по (ω) и (t) будет:
(δSi)` = π (Ri*sin ωi*t+φ)^2*)`ω + π (Ri*sin ωi*t+φ)^2*)`t =2π* ωi*Ri^2*cos (ωi*t+φ) δt+ 2π *t*Ri^2*cos (ωi*t+φ)δω;
Данное ускорение характеризует вихревые свойства приливного ускорения и его величина определяется элементами вращения первого тела;
(δSi)` =2π* ωi*Ri^2*cos (ωi*t+φ)δt + 2π *t*Ri^2*cos ωi*t+φ)δω;
Изменение расстояния между концами радиусов вращающихся тел, если тела вращаются в одинаковом направлении, составит:
δR = Rj *cos (ωj*t + φj) — Ri*cos (ωit* +φi)
δR — является функцией переменных (ω),(t) производная выражения будет:
δR = (Rj *cos (ωj*t + φj) — Ri*cos (ωit* +φi))`ω + (Rj *cos (ωj*t + φj) — Ri*cos (ωit* +φi))`t = [Rj *ωj*sin (ωj*t + φj) — Ri*ωi*sin (ωit* +φi)] δt+[(Rj *sin (ωj*t + φj) — Ri*sin (ωit* +φi)]δω
Изменение расстояния между концами радиусов вращающихся тел характеризует поступательные (волновые) свойства взаимодействия.
В формуле [2] имеется промежуточная переменная (R), при дифференцировании выражение приливного ускорения примет вид (производная частного):
w = ( G*Mi/R^2)` = ρ* G*δSi *δR/R^2 = -2 ρ* G*δSi *δR / (R^3
w = 2π * ρ*G*[ ωi*Ri^2*cos (ωi*t+φ)δt + t*Ri^2*cos ωi*t+φ)δω] *[Rj *ωj*sin (ωj*t + φj) — Ri*ωi*sin (ωit* +φi)] δt+[(Rj *sin (ωj*t + φj) — Ri*sin (ωit* +φi)]δω/ R^3
Приливные ускорения связывают пространство, время, энергию и материю:
wj = (aj)` = f (R,t,ω,Μ)`
С ростом порядка производной и уменьшением расстояния между телами приливные ускорения увеличиваются, что объясняет жесткость связей атомных ядер.
Энергия при этом может переходить из энергии поступательного (волнового) движения тела (mV^2=mc^2 ) в энергию вращательного (вихревого) движения тела ( m(ω*R)^2=mc^2). Процесс этот носит колебательный характер и продолжается до полного израсходования энергии. Наиболее наглядно этот процесс изображен на [фиг.2] взятой из книги В.А. Ацюковского «Эфиродинамика». Капли капают в раствор и после поступательного движения превращаются в вихри… .
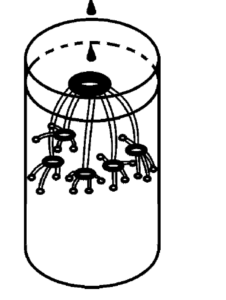
Аналогично черные дыры излучают джеты, которые превращаются в вихри.
Превращением энергии из поступательного движения в вихревое объясняется дуализм материи, как единство волновых и вихревых её свойств. Материя бесконечна, так как любой из вихрей состоит из волн, а любая волна состоит из вихрей и это не мешает присутствию бесконечно малого в бесконечно большом, чем и объясняется многообразие природы. Минимальная частица материи-это тоже вихрь, состоящий из волн но более плотный чем его предшественник, а следующий будет еще плотнее. Переходя к бесконечно большим величинам, можно предположить, что Наша Вселенная плотнее чем окружающий космос и произведение (ω*t) определяет её расширение до полного израсходования энергии (ω), после чего начнется процесс схлопывания под действием сил притяжения, которые никто не отменял.
