Взаимодействие вращающихся тел осуществляется посредством гравитационных волн, существование которых наукой в последнее время доказано (11 февраля 2016 года). Средой в которой осуществляется взаимодействие является физический вакуум ( плотность 400 — 500 фотонов на см.^3; T = 2,725 K; F = 160 Ггц.). Источником гравитационных волн является любое тело, совершающее ассиметричное движение относительно другого тела в его гравитационном поле, при этом излучение идет с круговой направленностью в полосе частот от (F -ω1) до ( F + ω1); (F -ω2),(F + ω2)
где : ω1 , ω2 — угловые скорости вращения взаимодействующих тел;
Воздействие гравитационных волн происходит только со стороны взаимодействующего тела от которого происходит и отражение собственных волн. Это определяет направленность гравитационного взаимодействия. В результате интерференции возникает стоячая приливная волна, которая обладает свойством менять направление в зависимости от соотношения угловых скоростей взаимодействующих тел. Приливная волна возбуждается в разных материалах с разной силой и оказывает на тела разное действие. Это действие, в первую очередь, зависит от структуры поверхности взаимодействующих тел.
В современной науке рассматривают четыре вида взаимодействия: сильное, слабое, гравитационное и электромагнитное. При этом гравитационное взаимодействие рассматривается в таком виде, в каком его сформулировал И. Ньютон; то есть в статическом состоянии невращающихся тел.
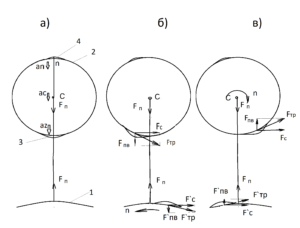
Взаимодействие вращающихся тел рассмотрим на примерах, изображенных на рисунках а), б), в) [ фиг.1 ]. Малое тело (2) находится в гравитационном поле большого тела (1). На малом теле возникают приливные волны на освещенной стороне (3) и на теневой стороне (4). Приливная волна на освещенной стороне определяет результирующее действие, так-как превосходит по величине приливную волну на теневой стороне.
При отсутствии вращения двух тел относительно друг друга взаимодействие их определяется взаимным притяжением силой (Fп) в соответствии с Законом всемирного тяготения [(рисунок а.) фиг.1], при этом ускорения, действующие в различных точках тел зависят от удаленности точек от источника притяжения:
δw zi = а zi — а ci (для точки зенита) [1]
δw ni = a ni — a ci (для точки надира)
где: a ci – ускорение центра тела;
Ускорение в δw zi > δw ni ,
так как зенит ближе к телу ( 1) чем надир. Разница в их величине вызывает дополнительное движение тела (2) в сторону тела (1) с ускорением, которое в теории ОТО А. Эйнштейна характеризуется как дополнительное искривление пространства вблизи массивных тел;
w = δw zi — δw ni
Это приливное ускорение, которое необходимо рассмотреть более подробно.
При вращении большого тела при неподвижном малом теле или вращении малого тела с меньшей скоростью чем скорость большого существует явление подкручивания, выражающегося в увеличении скорости малого тела (рисунок б.) вследствие того, что приливная волна увлекает за собой малое тело. Сила трения — Fтр увеличивает скорость вращения малого тела при помощи проекции -Fc и появляется проекция силы трения — Fпв — сила приливной волны притягивающая малое тело к большому. Эта сила действует вне зависимости от силы взаимного притяжения.
При вращении малого тела со скоростью большей чем скорость большого тела наблюдается явление торможения, выражающееся в уменьшении скорости малого тела и в отталкивании малого тела от большого силой Fпв ( рисунок в.). Рисунки б) и в) идентичны, но рассматривают взаимодействие со стороны малого тела (2), так как доказательство истинности закона основано на взаимодействии Земли (2) и Солнца (1), которое приведено в записи «Теория приливной волны».
В соответствии с законом всемирного тяготения все тела взаимно притягиваются с ускорением, которое рассчитывается для тела (2) по формуле
a2 = G*M1/R^2[2]
где:
G -гравитационная постоянная
М1 -масса небесного тела (1)
R — расстояние до небесного тела
По своей физической сути приливное ускорение является полной производной от ускорения по расстоянию и времени.
w = (а)` = f ( R )` [3]
Продифференцировав выражение [2] по расстоянию (для наглядности берется только первая производная) получим:
w2= (a2)` = da2/dR ; w2 = -2G1*M1 dR/R^3 [4]
Из выражения [4] видно, что на величину приливного ускорения влияют массы тела (1), находящиеся в обратной зависимости от куба расстояния (не от квадрата), а это поверхностные массы. Поэтому возможно представить, что эти массы вращаются по радиусам близким к радиусам взаимодействующих тел, тогда изменение расстояния между взаимодействующими массами можно представить как:
δR = R1* cos (ω1* t+ φ1) — R2cos(ω2* t+ φ2)
где:
ω1, ω2 — угловые скорости вращения;
φ1, φ2 — начальные углы вращения;
R1, R2 — радиусы небесных тел;
δR = f (t , ω );
(R)` = [R1* cos (ω1* t+ φ1) — R2cos(ω2* t+ φ2) ] ` [5]
Выражение [5] является сложной функцией из-за наличия члена (cos ω*t +φ)` =- ω*sin ω*t +φ),
Для простоты понимания берется только первая производная, однако на практике могут быть взяты и производные других порядков и составлены тригонометрические ряды из них.
dR/dt = — R1*ω1* sin (ω1* t+ φ1) + R2*ω2*sin(ω2* t+ φ2) [6]
w2 = 2G1*M1*[ R1*ω1* sin (ω1* t+ φ1) — R2*ω2*sin(ω2* t+ φ2)]/R^3 [7]
аналогично;
w1 = 2G1*M2*[R2*ω2* sin (ω2* t+ φ2) — R1*ω1*sin(ω1* t+ φ1)] /R^3 [8]
где: G1- гравитационная постоянная для первой производной ускорения. Гравитационная постоянная учитывает и то обстоятельство, что радиусы вращения взаимодействующих масс и радиусы тел имеют различия.
Анализ выражений [7] и [8] показывает важную особенность приливных ускорений, их зависимости от угловых скоростей вращения взаимодействующих тел. При скоростях в миллиарды оборотов в секунду, что характерно для микромира, эти ускорения приобретают громадные значения.
В общем виде формула ускорения для тела вращающегося в гравитационном поле центрального тела имеет вид:
а1 = M2 {(G/R^2) + (G1/R^2)` +[(G2/R^2)`]`….+ [(Gn/R^2)`] `(n) } [9]
где: G, G1, G2…Gn — гравитационные постоянные при производных соответствующих порядков;
M2 — масса центрального тела;
R — расстояние до центрального тела;
В общем виде w1`(n) = (n+1)*Gn*M2*[R2*ω2^n* sin( ω2*t +φ ) — R1*ω1^n* sin (ω1* t+ φ1)/R^n+1 [10]
где: w`(n)-производная n-порядка
Анализ этой формулы показывает, что с ростом порядка производной числитель стремится к бесконечно большой величине, а знаменатель стремится к бесконечно малой величине и общее значение стремится к бесконечно большой величине, что объясняет очень жесткое действие приливных сил на малых расстояниях.
В выражении [2] a2 = G*M1/R^2, которое сформулировано по теории И. Ньютона, появились новые члены:
2G*M1*R1*ω1*sin(ω1*t+φ1 )]/R^3- более известен как дополнительное искривление пространства вблизи массивных тел ОТО А.Эйнштейна. А. Эйнштейн не понял, что это искривление обусловлено вращением первого тела.
-2G1*M1[R2*ω2*sin(ω2t+ φ2)/R^3 — предсказанное академиком А.Д. Сахаровым влияние на ускорение второго тела.
Величина угловой скорости вращения (ω) является величиной переменной и в ряде случаев это необходимо учитывать и брать частную производную и по (ω)
dR/dω = — t* [R1* sin (ω1* t+ φ1) + R2*sin(ω2* t+ φ2)]
Приливные ускорения является функцией времени (ω*t). Скорее всего и наша Вселенная ускоренно расширяется под действием приливных ускорений. Ускоряться она будет не бесконечно, рано или поздно энергия базовых элементов вселенной закончиться и приливные ускорения просто пропадут, останется только ускорение взаимного притяжения, а оно никуда не пропадет.
Важнейшим вопросом в дальнейшем продвижении закона является определение гравитационных постоянных. Прежняя гравитационная постоянная (G) была определена из условий взаимного притяжения на Земле и уже в самом методе могли быть погрешности и взяты поправки на действие приливных сил.
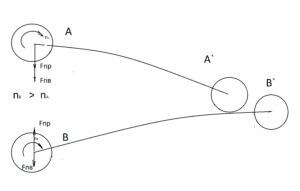
В соответствии с указанным законом происходит формирование спиралей галактик и вселенной. На рисунке (фиг.2) изображено формирование спирали двумя космическими телами с разными угловыми скоростями вращения. Тело А притягивается к телу В силой взаимного притяжения Fпр и силой притяжения приливной волны Fпв, при этом тело В притягивается к телу А силой взаимного притяжения Fпр, но отталкивается силой силой приливной волны Fпв (именно эту силу иногда принимают ошибочно за антигравитацию). Важной особенностью совместного движения двух тел является то, что тело имеющее меньшую скорость вращения, будет всегда догонять тело, имеющее большую скорость вращения.
При взаимодействии трех тел картина представляется более сложной, но для компьютерной программы эта задача не является сложной.
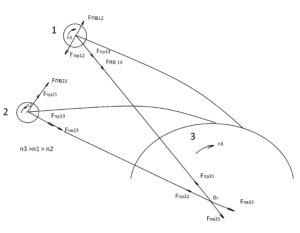
На рисунке (фиг.3) представлено взаимодействие трех тел, результатом которого является поглощение тел (1) и (2) телом (3), под которым подразумевается черная дыра галактики, имеющая большую скорость вращения. Тело (1) имеет скорость вращения большую чем тело (2), поэтому оно отталкивается от тела (2) силой приливной волны Fпв12 , но тело (2) притягивается к телу (1) силой притяжения приливной волны Fпв21, поэтому траектория тела (1)более пологая чем у тела (2). Вместе с тем тела (1) и (2) имеют взаимное притяжение силами Fпр12 и Fпр21. Тело (3) отталкивается при этом от обоих тел силами приливной волны F пв31, Fпв32, но притягивается силами притяжения Fпр31,Fпр32 . Силы Fпв31, F пв32 не вызывают перемещения черной дыры, потому что аналогичные силы действуют со всех сторон черной дыры, они лишь уплотняют материю черной дыры.
На рисунке тело (1) находится впереди тела (2) так-как тела с большей скоростью вращения пытаются занять место перед телом с малой скоростью вращения и это определяет их положение в рукаве спирали. В процессе формирования спирали галактики происходит уплотнение материи в рукавах и уменьшаются периоды орбит взаимодействующих тел.
Аналогичным образом задача решается и для большего количества тел. Использование теории приливной волны дает важный инструмент в руки разработчиков программ полетов искусственных аппаратов и специалистов занимающихся анализом орбит космических тел.
В законе рассматривается общий случай, когда очевидно, какое тело вращается быстрее, но в большинстве случаев определить это можно только путем специальных расчетов. Мерой сравнения являются ускорения гравитационных полей обоих тел приведенная к их поверхностям.
Приливные ускорения для двух взаимодействующих тел рассчитываются по следующим формулам ( Гравитационное взаимодействие и не слабое и не сильное. ):
w1 = 2G*M2*[ R1*ω1* sin (ω1* t + φ1) — R2*ω2*sin(ω2* t + φ2)] /R^3 [10]
для первого тела
w2 = 2G*M1*[ R1 *ω1* sin (ω1* t + φ1) — R2*ω2*sin(ω2* t + φ2)] /R^3 [11]
для второго тела
R — расстояние между центрами тел; -R1,R2 -радиусы тел;
ω1,ω2 — угловые скорости вращения;
M1,M2- массы тел;
G — гравитационная постоянная;
t — время.
эти выражения можно упростить, приняв R-R1 = R-R2 =R и зная, что V = Rω, можно сравнивать линейные скорости точек, приведенные к поверхностям тел;
ΔV1 = R1ω1 — R ω2 [12]
ΔV2 = R ω1 — R2ω2 [13]
В зависимости от соотношения ускорений (скоростей) могут быть различные варианты изменения скорости вращения тел и направления действия сил:
- -одно тело тормозит другое, а само подкручивается, при этом одно тело притягивает другое, а другое отталкивает это тело;
- -оба тела подкручивают друг друга, при этом тела взаимно притягиваются;
- -оба тела тормозят друг друга, при этом тела взаимно отталкиваются;
Три варианта указанных выше взаимодействий объясняют действие внутриядерных сил в химических элементах, которые носят приливной характер.
Незнание первого варианта гравитационного взаимодействия породило понятие слабого взаимодействия и вынуждает исследователей искать » пятую силу» и «антигравитацию» и «задача трех тел» до сих пор считается нерешенной.
Пары нуклонов взаимодействуют с другими парами в ядре, создавая цепь взаимодействий из всех пар нуклонов ядра с пространственной обратной связью (первый вариант) (рис.4)
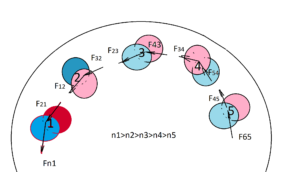
При высокой температуре и давлении происходит взаимное подкручивании нуклонов в паре, при этом нуклоны сближаются вплотную и могут запасать энергию вращения (второй вариант), которую потом будут отдавать, тормозя друг друга в реальных условиях космоса (третий вариант), одновременно удаляясь друг от друга, ослабляя хватку (рис.5) .
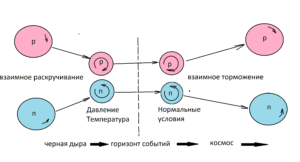
В любом случае общая кинетическая энергия вращающихся тел уменьшается за счет сил трения приливной волны. В твердых телах большая часть энергии приливной волны идет на нагрев тел, но приливные деформации проявляются и в этих телах.
Незнание второго и третьего вариантов гравитационного взаимодействия породило появление сильного взаимодействия, которое на деле являются лишь частью гравитационного. Приливные ускорения являются производными от гравитационных и имеют обратную зависимость от куба расстояния (для первой производной), что и послужило причиной ошибки.
А.Эйнштейн создавая свою теорию ОТО не рассматривал действие приливных сил и учел их действие на орбиту Меркурия за счет искривления пространства вблизи массивных объектов (Солнца). Задачу он решил, но с «заднего входа». Искривление пространства вблизи массивных объектов, по всей видимости, действительно существует, но смещение орбиты Меркурия не является доказательством искривления пространства, так как это следствие действия приливной волны.
Искривление пространства вблизи массивных тел доказывало бы материальность пространства, но это искривление надо еще доказать. Скорее всего на сверхплотные атомы пространства ( продукты производства «черной дыры» масштаба вселенной или даже выше) действуют приливные силы, отталкивая их от массивных тел. «Мух от котлет» надо будет рано или поздно отделить. Действие приливных сил — это одно, а искривление пространства это другое.
Закон взаимодействия вращающихся тел.
При взаимодействии двух вращающихся тел, имеющих общую плоскость вращения, в теле, гравитационное поле которого вращается с меньшей скоростью, другим телом индуцируются приливные волны, результатом действия которых является увеличение скорости вращения тела и притягивание его к другому телу, а в теле, гравитационное поле которого вращается с большей скоростью, другим телом индуцируются приливные волны результатом действия которых является уменьшение скорости вращения тела и отталкивание его от другого тела.
