Задача трех тел до настоящего времени не могла быть решена по той причине, что в расчетах отсутствовала одна из важнейших действующих сил — сила приливной волны, которая является силой универсальной, действующей на все тела и все среды. Эта сила действует самостоятельно и направление её зависит от соотношения скоростей вращения взаимодействующих тел. Для лучшего понимания силу приливной волны лучше рассматривать на примере земных приливов и отливов, но результат действия силы аналогичен и в очень твердых телах, просто в твердых телах приливная волна создает зоны высокой и низкой плотности, вызывающие нагревание или охлаждение тела, при этом повышается или понижается скорость вращения электронов в атомах тела и сила их отталкивания (притяжения) от гравитационного поля другого тела. Сила приливной волны действует как на объекты микромира, так и на объекты макромира имеющие вращение в гравитационном поле.
Наиболее наглядно решение задачи трех тел представлено природой при формировании спиралей галактик с образованием черных дыр (фиг.1).
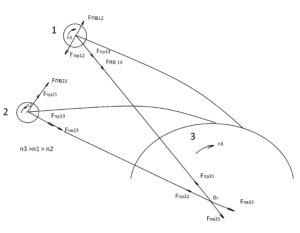
На рисунке (фиг.1) представлено взаимодействие трех тел, результатом которого является поглощение тел (1) и (2) телом (3), под которым подразумевается черная дыра галактики, имеющая большую скорость вращения. Тело (1) имеет скорость вращения большую чем тело (2), поэтому оно отталкивается от тела (2) силой приливной волны Fпв12 , но тело (2) притягивается к телу (1) силой притяжения приливной волны Fпв21, поэтому траектория тела (1)более пологая чем у тела (2). Вместе с тем тела (1) и (2) имеют взаимное притяжение силами Fпр12 и Fпр21. Тело (3) отталкивается при этом от обоих тел силами приливной волны F пв31, Fпв32, но так как силы приливной волны подобного типа действуют со всех сторон роторной части черной дыры, то перемещения ротора не происходит, а происходит уплотнение вещества роторной части с повышением его температуры до условий термоядерного синтеза.
Решение задачи сводится к решению дифференциальных уравнений движения тел:
G M2/R12^2 + (G M2/R12^2)`+ (G M2/R12^2)` ` … + а1-2 = a12
G M3/R13^2 + (G M3/R13^2)`+ (G M3/R13^2)` ` … + а1-3 = a13
G M1/R12^2 + (G M1/R12^2)`+ (G M1/R12^2 )` ` … + а2-1 = a21
G M3/R23^2 + (G M3/R23^2)`+ (G M3/R23^2)` ` … + а2-3 = a23
G M1/R13^2 + (G M1/R13^2)`+ (G M1/R13^2 )` ` … + а3-1 = a31
G M2/R23^2+ (G M2/R23^2)`+ (G M2/R23^2)` ` … + а3-2 = a32
где: а1-2… а3-2 — начальные ускорения тел;
a12 … a32 — полные ускорения тел;
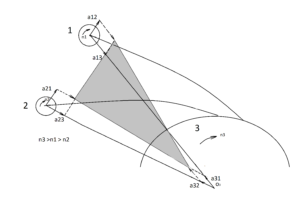
Решение задачи производится циклами. В каждом новом цикле учитываются результаты (R 12 i, R13 i, R23 i ) , полученные в предыдущих циклах. На рис.3 показан пример одного цикла вычислений по предыдущему примеру. Серым цветом выделен треугольник, полученный по результатам одного цикла вычислений.
В настоящее время нет данных о величине гравитационной постоянной для производных различных порядков, поэтому она у всех производных принята равной.
