Условием устойчивости к возмущениям гироскопических систем считается соблюдение в их работе периода колебаний, известного как период Шулера.
Тш = 2π (R/g)^-2 = 84,4 min. [1]
где:
R — радиус Земли;
g — ускорение свободного падения;
В реальных условиях носители гироскопических устройств имеют отличия параметров от номинальных для невозмущенного состояния в виде δR и δg [фиг.1], что вызывает появление возмущений. Приливные ускорения оказывают возмущающее действие на работу гироскопических систем. При этом: g-g`=δg=w; R2-R=δR
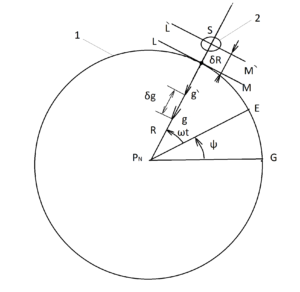
Приливные ускорения вычисляются по формуле:
w = 2G*M [ R1*ω1* sin (ω1 t + φ1) — R2* ω2* sin (ω2 * t +φ2)] / R^3 [2]
где:
G = 6,67 10 ^-11 m^3/ kg sec^2 -гравитационная постоянная;
R = Удаление гироскопической системы от центра Земли;
R1 = 6,37 10^ 6 m -радиус Земли;
М1 = 5,97 10^24 kg. — масса Земли;
T1 = 60*60*24 sec – период вращения Земли;
ω1 = 2π/Т — угловая скорость вращения Земли.
ω2 = угловая скорость вращения гироскопической системы;
R2 — радиус вращения гироскопической системы;
Анализ уравнения показывает, при каждом возмущении появляется составляющая приливного ускорения направленная вертикально. При R = R1 = R2 ; ω1= ω2 условия формулы [1] соблюдается, так как w = 0. Есть вариант R1*ω1 = R2ω2., при этом создаётся дополнительное вращение гироскопической системы со скоростью ω2 =R1* ω1/R2, что принципиально возможно. Такая возможность имеется, например, в ИНС геометрического типа, для этого необходимо лишь изменить алгоритм работы. При других значениях аргументов условия не возбуждения трудновыполнимы, поэтому возможен только учет приливных ускорений в работе гироскопических систем.
Уменьшаемое 2G*M [ R1*ω1* sin (ω1 t + φ1) в выражении [2] представляет из себя постоянную, характеризующую гравитационное поле Земли. Все изменение приливного ускорения идет за счет изменения вычитаемого — R2* ω2* sin (ω2 * t +φ2), причем величина R2 может быть вычислена измерением высоты (или глубины) как R2 = R + δR. Если произвести измерение вертикальной составляющей приливного ускорения, то можно получить величину в которой содержится информация о ω2- угловой скорости возмущения, пропорциональной ошибке в навигационном параметре.
wi = 2G*M [ R1*ω1* sin (ω1 t + φ1) /( R+δR)^3 — (R+δR)* ω2* sin (ω2(i-1) * t +φ2)] / (R+δR)^3
откуда:
ω2 = 2G*M [ R1*ω1* sin (ω1 t + φ1) /( R+δR)^3 — wi ] * (R+δR)^3/ (R+δR)* sin (ω2(i-1) * t +φ2)]
ΔНП = — f (ω2)- поправка навигационного параметра.
В настоящее время снижение возмущений производится с использованием демпфирования колебаний с помощью посторонних источников информации о параметрах движения гироскопических систем. Отличие существующих способов демпфирования в том, что они не рассчитывают полный тригонометрический ряд приливных ускорений, состоящий и из производных высших порядков от формулы всемирного тяготения И. Ньютона, которые оказывают наиболее жесткое воздействие.
